OPINIONES
–
El espacio
Introducción
A raíz de consultarnos en cierta ocasión sobre el concepto de entropía llegamos a la conclusión de que no sin cierta razón tantos eminentes científicos han declarado como no digna de consideración cualquier hipótesis que niegue algún principio de la termodinámica.
Teníamos la idea de que la termodinámica era el estudio del calor, la temperatura, y las máquinas térmicas, y efectivamente de estas cosas se ocupa entre otras muchas; pues la termodinámica tiene que ver con todo.
La termodinámica esel estudio de la energía y de las leyes que gobiernan sus transformaciones; por lo que está presente y determina todos los procesos, cambios o fenómenos.
Nos percatamos entonces que en nuestra formación reconocíamos, en general, principios y leyes por autoridad. Aceptando como verdadero todo lo que fuera útil en su campo de aplicación. Esta posición, aunque valida en términos tecnológicos y de ciencia aplicada, no lo es en condiciones menos apremiantes en cuanto a soluciones, con metas más ambiciosas de generalidad y formalización. Pienso que debemos tener claro:
- Que es comentario, información, o descripción
- que reconocemos como principios generales trascendentes.
- que sabemos y bajo qué condiciones.
- que aceptamos como útil en marcos limitados; aunque sabemos contradictorio.
- que es especulación dentro del panorama de lo posible.
- y que, sencillamente, resulta absurdo.
Resulta positivo que el lector aguze su pensamiento, y reflexione en detalle sobre cada una de las ideas expuestas, que finalmente colocará en cada una de las categorías anteriores (para el), otros lectores podrán sin duda en función de sus reflexiones, experiencias, conocimientos, etc, hacer otras clasificaciones. Se recomienda hacer búsquedas en los temas de interés que aparecen relacionados en estas páginas.
Por tal motivo un asunto tan general como la consideración de la entropía a escala de todo el universo nos llevó a pensar, quizás por falta de una sólida preparación; pero también por la ausencia de una teoría sin inconsistencias, que debíamos comenzar por las bases más elementales del edificio de la física, y al hacerlo nos percatamos, entre maravillados y asombrados, que ahora, razonando, es que empezamos a comprender, al menos mejor, lo que antes aceptábamos bajo criterios de utilidad.
Aun cuando la física no se construye en su totalidad sobre la mecánica, exclusivamente, no es menos cierto que todas sus ramas; aun las que se consideran más divorciadas de ella, utilizan de alguna forma sus leyes y conceptos, y no siempre modificados. Por eso comenzaremos nuestros estudios por ella.
ESPACIO y TIEMPO son dos conceptos comunes a todo fenómeno. ¿Qué podemos decir de ellos en forma directa y elemental? veámoslo, sin que ello se considere nuestra única o última palabra, continuamente volveremos sobre el tema. EL ESPACIO y EL TIEMPO se considerarán desde la física y las matemáticas; pero también pueden, y deben serlo,desde el arte, la psicología, y la mística.
EL ESPACIO
El tiempo y el espacio son esquemas con arreglo a los cuales pensamos y no condiciones en las que vivimos. A. Einstein (Muy muy profundo)
Lo que puede muy bien ser cierto; pero entonces dicho arreglo responde a una realidad oculta, a la cual representa con probada eficacia.
PRIMEROS ELEMENTOS
- Digamos que el espacio es el lugar donde se encuentran (existen) los cuerpos.
- Cuerpo es una porción limitada de materia. llamamos materia a la sustancia[1] de que están hechos los cuerpos.
- Dos cuerpos no pueden ocupar el mismo lugar en el espacio.
- Como otros conceptos primarios[2] es indefinible con exactitud y sin caer en tautologías; pero medible.
- Medimos el espacio introduciendo en el mismo un sistema de referencia, generalmente de ejes coordenados. Este solo puede introducirse situándolo en un cuerpo o refiriéndolo a éste.
- Solo a partir de los cuerpos puede introducirse una métrica en el espacio.
- Bastan 3 ejes para poder identificar cualquier punto del espacio, o sea, el espacio se caracteriza por poseer 3 magnitudes independientes.
- Al número de magnitudes necesario para caracterizar completamente, al menos en determinados aspectos, una cosa, se le llama grados de libertad de esa cosa.
- ¿Solo tenemos conciencia del espacio por los cuerpos que se encuentran en él? Si cerramos los ojos y nos imaginamos flotando sin ningún cuerpo a nuestro alrededor podemos hacernos una idea del espacio. Dentro de una cueva, en la profundidad de la misma donde no llegue un atisbo de luz también podemos tener una impresión directa de lo que es el espacio. La impresión resulta, digamos, extraña, por no tener una palabra mejor para expresarla.
- Es la luz quien nos muestra la existencia de cuerpos en el espacio; porque, aunque el tacto puede informarnos de la existencia de un cuerpo, no podemos concebir el espacio a partir de él.
- Como la luz es un pequeño intervalo del espectro de radiaciones, pueden existir, y de hecho existen en el espacio, cuerpos o entes que no radien en este intervalo y que nos pasen inadvertidos.
- Imágenes de objetos espaciales construidas a partir de rayos infrarrojos, rayos x o radiación gamma nos dan hoy un nuevo aspecto de objetos ya conocidos; pero también nos presentan otros nuevos, y a partir del comportamiento gravitatorio de cuerpos conocidos hemos tenido noticias de una llamada “materia oscura” a la que no podemos directamente acceder ni sabemos bien que es.
- Ya el espacio nos pone claro que lo que el “yo” puede conocer del “no yo” es una parte del mismo, en los términos que determina nuestra particular constitución; pero que crece en la medida en que con nuestra razón y experiencia ampliamos nuestra percepción, o a través de la tecnología el alcance de nuestros sentidos.
ESPACIO Y MATERIA
- Pero ese espacio físico, ¿qué es? en zonas singulares del universo la densidad de la materia es grande; pero en casi todo éste la materia es inexistente y a pesar de su aparente solides, en el espacio que ocupan los cuerpos reina el vacío.
- En el núcleo atómico, donde la materia no se da a conocer como sustancia, sino como ladrillo elemental del átomo, se concentra prácticamente toda la materia.
- La materia en el átomo se encuentra extraordinariamente concentrada en el núcleo, su densidad es prácticamente constante para cualquier elemento y es del orden de 105 ton/mm3, cien mil toneladas por milímetro cubico. Como la densidad de los cuerpos más pesados constituidos por platino o uranio es en el macro-mundo del orden de (1-2)10-8ton/mm3, resulta que la materia ocupa solamente de una a dos partes, en 1013, del volumen total del cuerpo.
- Como término de comparación sirva decir que si suponemos el diámetro del núcleo igual a 1cm. El del átomo sería de 100 m.
- No obstante estar la materia muy concentrada en el núcleo, en el cuerpo esta uniformemente distribuida por estarlo los átomos en el mismo. Idéntica situación se presenta en el universo como un todo, con respecto a las grandes concentraciones de materia.
- los volúmenes espaciales serán homogéneos dependiendo de la extensión que ocupa el fenómeno. Por ejemplo: podemos considerar el volumen de espacio limitado al núcleo como homogéneo; pero las condiciones del núcleo no se extienden mucho más allá del mismo. Si bombardeamos una delgada lámina metálica con partículas alfa, las partículas que pasan lejos de los núcleos atravesaran la lámina, mientras las que pasan cerca serán desviadas proporcionalmente a su proximidad al mismo.
- El interior del átomo presenta unas características diferentes a la existente entre los átomos. De modo que las condiciones del micromundo[3] son diferentes de las consideradas en la escala espacial donde se desarrolla nuestra vida y a la que daremos el nombre de macromundo.
- Aunque los cuerpos están formados por enormes cantidades de átomos con su masa prácticamente concentrada en su núcleo, la enorme distancia existente entre los núcleos atómicos en comparación con su diámetro, y su distribución uniforme, hacen el espacio ocupado por el cuerpo homogéneo a escala del macro-mundo.
- En el universo el espacio que rodea las grandes concentraciones de masa como las estrellas o huecos negros tiene un comportamiento diferente a las zonas donde apenas existe materia; pero en su totalidad la distribución de materia puede considerarse uniforme y el universo se considera homogéneo e isótropo[4].
Las condiciones espaciales donde se produce un fenómeno es dependiente de la extensión del mismo. Puede servirnos de comparación la aproximación lineal en un punto de una curva; que resulta valida únicamente si la variación alrededor del punto no sobrepasa ciertos límites.
En resumen, las condiciones o marco en que se produce un fenómeno están dadas, en el espacio en que se extiende el mismo, por la concentración de materia que se encuentra en dicho espacio.
Debido a las diferenciadas características que muestra el universo, según la escala que se considere, resulta conveniente dividirlo para su análisis en:
El micromundo en el interior del átomo. Menor o igual a 10-8 cm.
El macro-mundo: podemos considerarlo desde el átomo, incluyéndolo como un todo, hasta nuestro sistema planetario, convencionalmente tomado de un diámetro de 100 unidades astronómicas[5]. De 10-8 a 1016 cm.
El universo, el mundo en toda su integridad, a escala total. De los limites considerados al macromundo hasta los confines supuestos del universo. De 1016 a 1028 cm.
Aunque pudiera pensarse que el universo puede explicarse en función de las leyes de sus constituyentes más elementales, ÚNICAMENTE, esto no es cierto. Si así fuera, no sería necesaria la división anteriormente planteada, y que es fruto del desarrollo histórico del conocimiento del mundo.
El universo es uno solo; pero por ahora y posiblemente por siempre, habremos de dividirlo para conocerlo en los términos de la ciencia.
Considerar los hechos macroscópicos como valores medios de eventos microscópicos, como se hace en la teoría cinética de los gases, no es, EN GENERAL, posible.
El oxígeno y el hidrógeno son dos gases que responden a dicha teoría. Cuando se unen para formar el agua las propiedades de la nueva sustancia son básicamente producto de su estructura, más que de las características que mostraban sus componentes individuales.
ESPACIO Y GEOMETRIAS
Podría decirse que la geometría es el estudio de las formas y figuras con que la materia se da a conocer en el espacio y del espacio mismo. La geometría tiene una importancia y trascendencia tal en las relaciones del mundo que le dedicamos un capítulo aparte. Mencionaremos aquí solo algunas de sus más importantes vinculaciones.
El espacio como ya hemos dicho solo es medible en presencia de los cuerpos; pero podemos estudiarlo haciendo abstracción de la materia. La parte de las matemáticas conocida como geometría se ocupa de ello.
Los cuerpos se nos hacen presentes en el espacio por medio de las formas.
Llamamos forma al límite externo del cuerpo, a la superficie que encierra al mismo y por medio de la cual se manifiesta.
La geometría es el estudio de las formas, y del espacio que las contiene.
Las formas son en general complejas; pero de ellas extrae la mente las figuras simples que facilitan el estudio de las mismas.
¿El estudio de las figuras nos ayuda a comprender el espacio? Las formas pertenecen al cuerpo, no al espacio. No obstante del comportamiento de las figuras en diferentes superficies y en el espacio mismo, podemos hacer algunos descubrimientos sobre el espacio.
Las formas nos ayudan a comprender el espacio cuando las movemos, cuando las cambiamos de posición. ¿cómo afecta a las figuras su movimiento?
Ya que a las figuras no le suponemos ninguna característica material, éstas no se alteran por traslación ni rotación y el espacio se nos muestra INTRÍNSECAMENTE HOMOGÉNEO E ISÓTROPO,
Las relaciones internas de las figuras también se mantienen invariantes a los cambios de escala.
Las formas y figuras son esencias, se nos muestran con el auxilio de un soporte material que no constituye, la esencia, en sí misma.
LAS ESENCIAS SON LAS CARACTERÍSTICAS
POR MEDIO DE LAS CUALES SE MANIFIESTAN
LOS CUERPOS.
AQUELLO A TRAVES DE LO CUAL
CONOCEMOS EL MUNDO.
A LAS QUE SOLO ACCEDEMOS
APLICANDO LA ABSTRACCIÓN
A NUESTRAS EXPERIENCIAS.
Podemos concebir el espacio en una mayor generalidad matemáticamente. Contrastando el espacio físico, con las concepciones geométricas, ¿podríamos establecer la geometría del espacio físico?
La geometría de Euclides, hasta hoy, parece ser la geometría del espacio físico, por eso se sigue enseñando más de 2200 años después de su concepción.
Otras geometrías son de utilidad, especialmente cuando estudiamos las figuras con dos grados de libertad sobre superficies que no son planas,
La geometría euclidiana es la que, en dos dimensiones, se cumple en el plano. Una superficie a la que se le considera un radio de curvatura infinito, o lo que es lo mismo, una superficie sin curvatura.
En la superficie de la esfera, por ejemplo, no se cumple la geometría euclidiana y se construye una nueva geometría, la geometría esférica, de gran importancia en los trabajos geodésicos. La esfera es una superficie de curvatura constante. Presenta la misma curvatura en todos sus puntos, cualquiera que sea la dirección que escojamos. De acuerdo con lo dicho esta superficie se nos presenta también como homogénea e isótropa.
Sin embargo, en ella no se mantienen las relaciones intrínsecas de las figuras con cambios de escala. Por ejemplo, un triángulo en la superficie de la esfera se presenta euclidiano si sus lados son pequeños en relación con el radio de la esfera; pero deja de serlo si sus lados crecen proporcionalmente hasta hacerse comparables con el radio de la esfera.
Por extensión, EL ESPACIO EUCLIDIANO, se considera de curvatura infinita[6], y al espacio no euclidiano se le considera algún valor de curvatura, no necesariamente constante.
Para los espacios no euclidiano se han desarrollado nuevas geometrías.
Algunos fenómenos que se presentan alrededor de grandes concentraciones de materia[7] se han interpretado suponiendo que los fuertes campos gravitacionales afectan la curvatura del espacio[8], y han dado lugar a la aplicación de nuevas geometrías al espacio físico.
“Einstein en 1917 describió una teoría de la gravitación y de la geometría, La Teoría General de la Relatividad, que predecía en acuerdo cuantitativo con las observaciones, precisamente los dos efectos señalados en la referencia 5, Estas son las dos demostraciones cruciales de las predicciones geométricas de la teoría. A pesar de tan escasa prueba la esencial sencillez de la teoría general ha hecho que esta sea ampliamente aceptada.” (1)
Pero esta no es la única interpretación posible de los fenómenos señalados que indudablemente son producto del campo gravitacional, y se pueden explicar a partir de éste sin suponer el cambio de curvatura del espacio.
“El radio de curvatura del espacio físico no es menor de 1023 cm.(aproximadamente 105 años luz[9]) desconocemos si el universo a escala mayor no será plano[10]. Por triangulación se demuestra que el radio de curvatura no es menor de 1019cm.” Aproximadamente 10 años luz. (1)
“A escala menor ha quedado establecido que los rayos de luz se curvan ligeramente cuando pasan cerca del borde del sol. Esto significa simplemente que la luz se mueve con una trayectoria curva cerca del sol; pero en sí mismo no significa que la única interpretación sea que el espacio alrededor del sol sea curvo” (1)
“A partir de mediciones astronómicas llegamos a la conclusión de que la geometría euclediana proporciona una descripción extraordinariamente buena de las medidas de longitud, áreas, y ángulos, al menos hasta que alcancemos las enormes longitudes de 1027cm.” O aproximadamente 10 000 millones de años luz.” (al universo se le supone 14 000 millones de años de existencia) (1)
“En el mundo subatómico sin dar lugar a ninguna de las paradojas propias de éste, la teoría euclidiana ha resistido el ensayo experimental hasta 10-13cm. el diámetro del átomo es del orden de 10-8cm.y el del núcleo de 10-12cm. Todavía quedan muchos hechos por entender pero ninguno parece presentar contradicciones con la consideración de un espacio euclidiano”. (1)
Debemos señalar que la geometría analítica al establecer una relación entre el álgebra y la geometría permite extrapolar objetos algebraicos al campo de la geometría como los espacios de más de 3 dimensiones, que si por una parte permiten un tratamiento algebraico con toda rigurosidad, por otra carecen totalmente del sentido geométrico habitual. Resultan muy difíciles o imposibles de imaginar.
El lado práctico de las cosas es siempre más fácil de conceptualizar y explicar. Luego a partir de simples asunciones de naturaleza intuitiva, a las cuales aplicamos la lógica de la razón, llegamos a complejidades inimaginables que los experimentos nos dirán si se corresponden o no con el mundo;
pero siempre queda en los orígenes un sustrato de preguntas que no contestamos y que el desarrollo de la asignatura tampoco nos sirve para dilucidar.
Cuando estudiemos la relatividad abundaremos más sobre las geometrías no euclidianas.
LAS SIMETRIAS ESPACIALES
En el espacio se considera que no existen puntos destacados ni direcciones singulares. Todos los puntos y todas las direcciones son iguales y tienen “derechos iguales”. Esto es lo que se conoce con el nombre de simetría espacial.
por eso establecemos que los experimentos físicos realizados en diferentes lugares y con distinta orientación de los aparatos dan los mismos resultados.
La homogeneidad del espacio sustenta su simetría respecto a los desplazamientos. Su isotropía la sustenta respecto a los giros.
Manifestada geométricamente por la invariancia de las figuras en las traslaciones y los giros.
Pero cuidado, el ambiente que rodea estos experimentos debe ser el mismo; porque la distribución de la materia altera el comportamiento de los cuerpos, yo prefiero, por el momento,decir que establece el marco quedetermina las condiciones del experimento.
NINGUN FENÓMENO ES AJENO
A LAS CIRCUNSTANCIAS QUE LO RODEAN.
Las simetrías espaciales son la causa de la conservación del momento lineal y el momento cinético.[11] Y en colaboración con la simetría temporal, de la conservación de la energía.
La simetría espacial se cumple con absoluta rigurosidad en el macro-mundo. El universo contiene infinidad de macro-mundos y los macro-mundos están constituidos por infinidad micro-mundos.
En 1915 la matemática alemana Emmy Noether demostró el teorema que explica la conexión fundamental entre la simetría en física y las leyes de conservación, mostrando que toda ley de conservación, (INVARIANCIA),en un sistema físico, proviene de alguna simetría del mismo respecto a las leyes que se consideran. (4)
El teorema determina las magnitudes conservadas para cualquier conjunto de leyes físicas que posea algún tipo de simetría continua.
Si en un sistema físico se conservan estas magnitudes,entonces el conjunto de leyes es de aplicación en el mismo.
Si el comportamiento de un sistema físico no depende de su orientación en el espacio, se dice que las leyes físicas que lo gobiernan tienen simetría de rotación. A partir de esta simetría, el teorema muestra que el momento angular del sistema debe conservarse.
No es el sistema físico en sí mismo el que necesita ser simétrico. Un cuerpo irregular que gira en el espacio conserva su momento angular a pesar de su falta de simetría.
ES LA SIMETRÍA DE LAS LEYES FÍSICAS
QUE GOBIERNAN EL SISTEMA
LA QUE ES RESPONSABLE
DE LA LEY DE LA CONSERVACIÓN.
Si un experimento físico da el mismo resultado en cualquier lugar, esta simetría explica la conservación del momento lineal.
El teorema de Noether es una herramienta fundamental en la física teórica porque: (4)
El mismo permite determinar las cantidades conservadas a partir de las simetrías observadas.
Las teorías desarrolladas para explicar nuevos fenómenos se procura que satisfagan el teorema de Noether para que se conserven algunas magnitudes. La confirmación de dicha conservación en la práctica sirve para corroborar o no la teoría.
ESPACIO Y MOVIMIENTO
Es un hecho que los cuerpos cambian de posición en el espacio, decimos entonces que los cuerpos se mueven. Llamamos movimiento al cambio de posición de los cuerpos en el espacio.
Debido a “6”, no es posible considerar el movimiento de un cuerpo, sino con referencia a otro cuerpo.
Es obvio que el cuerpo donde situamos el sistema de referencia estará en reposo con respecto a dicho sistema, pues de moverse lo hacen conjuntamente.
Aquí estudiaremos el movimiento en estado “estable”. Suena difícil y contradictorio; pero lo que queremos indicar es que no nos detendremos en el cómo (la cinemática) o por qué (la dinámica) cuando se produce el cambio de posición. Ambas cosas serán tratadas en otro capítulo, después que consideremos el tiempo. Examinaremos únicamente la trayectoria o desplazamiento tratando de no involucrar el tiempo en este primer acercamiento. Así es como se considera el espacio en la geometría, donde los cambios de posición son lugares geométricos y los sistemas de referencias se mantienen en reposo relativo.
ANTES DE COMENZAR ESTABLEZCAMOS
ALGUNOS HECHOS
SOBRE LA DIFÍCIL CUESTIÓN DE LOS SISTEMAS DE REFERENCIA.
En la tierra disponemos de infinidad de sistemas de referencia solidarios a la misma y que por estar en reposo relativo los unos con los otros medirán todos la misma trayectoria de los objetos que se consideren en su cercanía. En la práctica de los problemas cotidianos de nuestra vida la única dificulta consiste en seleccionar el sistema de referencia en el que las ecuaciones del movimiento aparezcan en su forma más simple. Parece sencillo; pero se requiere experiencia para hacerlo bien.
Los sistemas de referencia solidarios a la tierra son, por estar nosotros en ella, los más naturales, necesarios,y generalmente,convenientes, a pesar de los movimientos de rotación y traslación de la misma. Estos movimientos, desde otras consideraciones que veremos luego, pueden afectar la calidad del sistema de referencia; pero en la práctica de la inmensa mayoría de los problemas no tienen ningún efecto y cuando lo tienen estos pueden ser corregidos.
Por necesidad, las mediciones y observaciones astronómicas se realizaban desde la tierra; aunque ocasionalmente conviene llevar estas a sistemas de referencia exteriores como cuando referimos el movimiento de todos los planetas a un sistema de referencia situado en el sol, lo que nos simplifica mucho la comprensión de nuestro sistema planetario.
Un sistema de referencia puede ser establecido en un cuerpo, pero el mismo puede tener infinitas orientaciones en el espacio, orientaciones que cambiarán con el movimiento del cuerpo. ¿Cómo seleccionar una orientación fácilmente reproducibley que no se altere con el movimiento de la tierra?
Un sistema orientado a una estrella fija muy lejana, aun cuando no mantenga, ESTRICTAMENTE, su orientación en su movimiento, ha demostrado ser lo suficiente preciso. Los sistemas orientados desde la tierra a las estrellas que se manifiestan fijas en el firmamento[12]mantienen su orientación aun en extremos opuestos de la órbita de la tierra alrededor del sol. Estos sistemas se conocen como inerciales y serán considerados nuevamente cuando estudiemos el movimiento.
Dado 2 cuerpos; que se mueven uno con respecto al otro, atendiendo solo al desplazamiento, es imposible decir cual se mueve y cual está en reposo, o si ambos se mueven. Desde cualquier asunción podemos justificar lo observado.
Ver fig. 1 (a), (b) y (c)
Si acompañamos cada punto observado con su distancia al sistema de referencia, todos los sistemas EN REPOSO RELATIVO manifiestan una única trayectoria; pero expresada de diferentes maneras en cada sistema.
Ver fig. 2. y 3
En general los desplazamientosOBSERVADOS dependen del sistema de referencia, o sea, del cuerpo con respecto al cual se considere. No sin razón llamamos a este movimiento en astronomía, movimiento APARENTE.
Ver fig. 3 y 4
¿Cuál es la expresión valida de la trayectoria en los diversos sistemas en reposo relativo? TODAS LO SON, pues refieren el mismo lugar geométrico.
Estos sistemas se comportan como diferentes idiomas que expresan con distintos fonemas una misma cosa.
¿y cuando existe un movimiento relativo entre ellos? Entonces resulta diferente, en general, para cada uno de ellos la trayectoria. No obstante para cada par “sistema de referencia cuerpo”, existe una única trayectoria posible que le es propia.
Cuando se considera el movimiento de un cuerpo respecto a una multiplicidad de otros cuerpos, es posible determinar el movimiento de este dentro del conjunto.
Los ejemplos de las figuras son extremadamente simples pues el movimiento del cuerpo se encuentra en un plano y los sistemas considerados tienen diferente posición; pero no se mueven uno con respecto al otro, o lo hacen de forma muy simple, con lo que las ecuaciones de transformación que permiten llevar los puntos de uno a otro sistema son muy sencillas. En general los sistemas pueden moverse de cualquier forma uno con respecto al otro, incluso con movimiento acelerado, y la trayectoria del cuerpo que se investiga ser espacial.
Se prueba en la mecánica analítica que siempre es posible hallar las ecuaciones de transformación para llevar las coordenadas de los puntos de uno a otro sistema con independencia del movimiento que exista entre ambos y del sistema de coordenadas adoptado. (5)
El criterio de validez, (de verdad) de algo, hay que referenciarlo, no es independiente del contexto de sus relaciones. Se ha de considerar siempre medio y fenómeno, sistema y lo que le rodea.
EJEMPLOS: Consideremos en la figura 1 (a) los cuerpos c1 y c2 que se ven mutuamente según la recta que los une. C1 en azul y C2 en rojo.
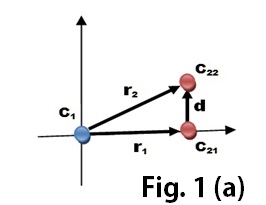
Localicemos en C1 el origen de nuestro sistema de referencia. Al comenzar a moverse C2 la visual desde C1 que lo localiza comenzará a elevarse hasta la posición final de C2, informando a C1 dicho movimiento. Esta misma visual que informa a C1 del movimiento de C2 le dice a un observador en C2 que es C1 quien se ha movido en sentido contrario pues la visual que se elevaba desde C1 se percibe bajando con respecto a la posición inicial, desde C2, El desplazamiento viene dado entonces por:
d = r2 – r1
Donde las letras r1 y r2 son los radios vectores de posición y “d” el vector desplazamiento.
Consideremos ahora, figura 1 (b) que es el cuerpo c1 quien se ha movido y con él el sistema de referencia. Entonces la visual habrá de
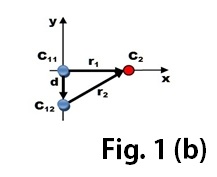
elevarse, con referencia a su posición inicial para poder seguir viendo a c2 y de esta forma a un observador en c1 le parecerá que es c2 quien se ha movido en sentido contrario al movimiento efectuado por c1 siendo el desplazamiento y la ecuación que lo expresa la misma que antes.
d = r2 – r1
Donde las letras r1 y r2 son los radios vectores de posición y “d” el vector desplazamiento.
Por ultimo podemos apreciar en la figura 1 (c) que idéntico resultado se obtiene si ambos cuerpos se mueven realizando en sentidos 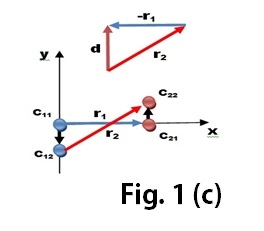 contrarios movimientos cuya suma sea igual al desplazamiento anterior.
contrarios movimientos cuya suma sea igual al desplazamiento anterior.
por lo que podemos afirmar que dado dos cuerpos[13] el movimiento que se aprecia desde cada uno de ellos es la diferencia del movimiento de ambos cuerpos sin que pueda decirse desde ninguno de ellos cual es el que se mueve y cual está en reposo o si los dos se están moviendo.
El movimiento de un cuerpo, por el hecho de tener que referirlo a otro cuerpo, y estar dado por la diferencia de los desplazamientos de ambos, tendrá un valor en general diferente para cada par de cuerpos considerados.
Esta relatividad no niega la objetividad de cada uno de estos valores.
Considérese por ejemplo la situación más cercana, dos automóviles que se mueven en sentidos opuestos tienen uno con respecto al otro una velocidad que es la diferencia de sus velocidades, teniendo en cuenta el signo de cada una, por lo que, si se mueven a igual velocidad, la velocidad de cada uno respecto al otro será el doble, y si se movieran en el mismo sentido, no se estarían moviendo uno con respecto al otro. No se confié, esto parece engañosamente simple; pero no lo es.
La descripción de las diferentes situaciones consideradas fue posible porque mirábamos el plano donde ocurrían desde el espacio donde 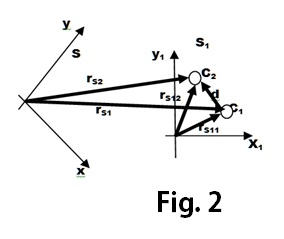 estaba, una dimensión superior. Desde el plano, sin salir de él, no podríamos adjudicarle el movimiento a uno u otro cuerpo.
estaba, una dimensión superior. Desde el plano, sin salir de él, no podríamos adjudicarle el movimiento a uno u otro cuerpo.
Sean los sistemas s1 y sde la fig. 2 el cuerpo C se mueve en el sistema s1 del lugar 1 al 2 y rS11 y rS12 son los respectivos radios vectores de posición en s1. El desplazamiento según los mismos será
d = rS12 – rS11
Desde S2 los radios vectores de posición son rS21 y rS22 y el desplazamiento
d = rS22 -rS21
Coincide con el de S1. TODOS LOS SISTEMAS EN REPOSO RELATIVO DETERMINARÁN DE IDÉNTICA MANERA CUALQUIER DESPLAZAMIENTO. Señalemos sin embargo que los ángulos que subtienden a “d” son, en general, diferentes desde cada sistema por lo que el tamaño aparente del desplazamiento no será el mismo.
Las diferencias entre el desplazamiento aparente y el real son más marcadas en el ejemplo de la figura 3. Sea un cuerpo que se mueve, con 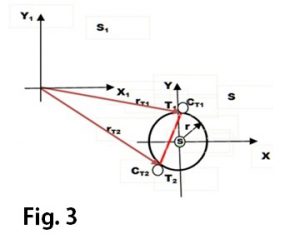 centro en el origen del sistema S, describiendo una circunferencia. Un observador en el origen de S verá el cuerpo moviéndose a su alrededor a una distancia fija al mismo de valor r. Desde el sistema S1 el movimiento del cuerpo se percibirá a simple vista como la ida y retorno del cuerpo entre los puntos de tangencia T1 y T2 Claro que si establecemos los correspondientes radio vectores de posición desde S1 al cuerpo, el observador en S1 se dará cuenta que la trayectoria que el percibe como las idas y retornos en un segmento de recta se trata en realidad de una circunferencia alrededor del origen de S. la ecuación del lugar geométrico del movimiento es en S
centro en el origen del sistema S, describiendo una circunferencia. Un observador en el origen de S verá el cuerpo moviéndose a su alrededor a una distancia fija al mismo de valor r. Desde el sistema S1 el movimiento del cuerpo se percibirá a simple vista como la ida y retorno del cuerpo entre los puntos de tangencia T1 y T2 Claro que si establecemos los correspondientes radio vectores de posición desde S1 al cuerpo, el observador en S1 se dará cuenta que la trayectoria que el percibe como las idas y retornos en un segmento de recta se trata en realidad de una circunferencia alrededor del origen de S. la ecuación del lugar geométrico del movimiento es en S
x2+ y2 – r2 = 0 y en S1
(x1)2 + (y1)2 – 2ax1 + 2by1 + (a2+b2– r2) = 0
de acuerdo con las ecuaciones de transformación
x= x1 – a y= y1 + b
donde “a” es la distancia entre los ejes de las “y” y “b” la distancia entre los ejes de las “x” ambos medidos a partir de S.
Las ecuaciones que describen el lugar geométrico del movimiento son diferentes; pero representan desde cada sistema la misma y única trayectoria.
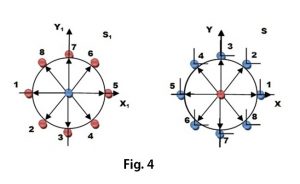
En la figura 4, a la derecha, podemos observar cómo se traslada el cuerpo en azul con el sistema de referencia S1 solidario al mismo, alrededor del origen del sistema S solidario al cuerpo representado en rojo. En la figura se representan 8 instantes en una rotación completa partiendo de 1 en sentido contrario a las agujas del reloj. A la izquierda se representa el mismo movimiento según seria percibido por el observador azul solidario al origen de S1 en el orden y el sentido en que son recogidos los 8 instantes de S vistos desde S1Nótese que todos los radios vectores que señalan las diferentes posiciones en S mantienen su módulo y dirección en S1pero invierten su sentido.
Esto se cumple cada vez que se intercambie la relación de reposo y movimiento entre los cuerpos considerados.
¿PODEMOS HABLAR DE UN DESPLAZAMIENTO EN EL ESPACIO ABSOLUTO?
Como pudo establecerse en ejemplos anteriores no sabemos cómo repartir el movimiento relativo entre dos cuerpos, en cada uno de los mismos. O sea, no sabemos quién se mueve y quien no o si los dos se mueven y en qué medida lo hacen. Solo desde el espacio una dimensión superior al plano de nuestro ejemplo pudimos asignarles movimientos a cada cuerpo considerado.
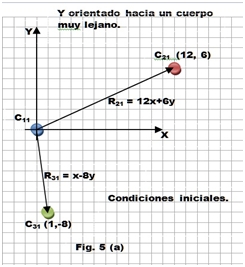
En la figura 5 (a) se han consideramos las condiciones iniciales de tres cuerpos c1, c2 y c3. El sistema de referencia orientado hacia) un cuerpo lejano lo hemos situado en c1 y respecto a él hemos trazado los radios vectores R21 y R31 que identifican las posiciones de c2 y c3 respecto al cuerpo c1
En la figura 5 (b) mostramos el mismo sistema y cuerpos luego de un desplazamiento intrínseco de cada uno.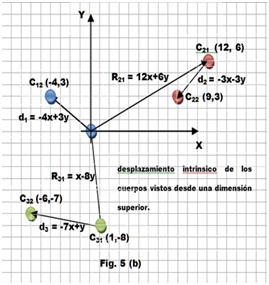
Desde c1 se supone que cuerpo y sistema no se han movido y los movimientos de c2 y c3 se percibirán como la suma de sus movimientos intrínsecos con el negativo del desplazamiento de c1 o sea: el desplazamiento del cuerpo 2 con respecto a 1 es igual al desplazamiento del cuerpo 2 menos el desplazamiento del cuerpo 1
D21 = d2 – d1
Y el desplazamiento del cuerpo 3 con respecto a 1 es igual al desplazamiento del cuerpo 3 menos el desplazamiento del cuerpo 1.
D31 = d3 – d1
Que expresan las relaciones que establecen los cuerpos a través de los desplazamientos.
Ver figura 5 (c)
Las operaciones entre vectores son independientes de los sistemas de referencia.
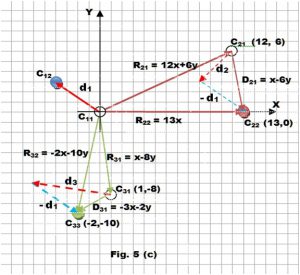
Pero para estar a cargo de lo ocurrido no es necesario conocer los movimientos propios de cada cuerpo. Considérese la figura 5 (d) y (e) en la que podemos apreciar claramente que a partir del sistema, que se ha movido a c12 y de los radios vectores correspondientes a cada cuerpo obtenemos los mismos desplazamientos de c2 y c3 que en la figura 5 (c).Esta es la forma en que se presentan las cosas en la experiencia.
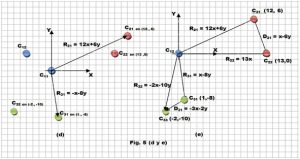
En (d) se vuelven a mostrar las condiciones iniciales y los desplazamientos intrínsecos y en (e) determinamos los desplazamientos. Estúdiese como la figura 5 (e) se corresponde perfectamente con la figura 5 (c)
¿Podría considerarse la posibilidad de encontrar los desplazamientos individuales? A partir de un análisis algebraico es posible plantear:
D21 = d2 – d1
D32 = d3 – d2 (1)
D31 = d3 – d1
Un sistema de 3 ecuaciones vectoriales con tres incógnitas, Cualquier otro cuerpo que consideremos se agregará al conjunto con una nueva ecuación independientepor lo que PARECERÍA que los desplazamientos intrínsecos o absolutos pudieran ser hallados para cualquier número de cuerpos.
¿Nos permitirá esto decir que las posiciones y desplazamientos relativos que hallamos coinciden con los absolutos?
NO, por dos razones:
Primera: aun cuando el movimiento de una multiplicidad de cuerpos puede ser determinada con respecto a otro cuerpo (el movimiento de los planetas alrededor del sol) o el de un cuerpo respecto a una multiplicidad de otros cuerpos, (el de la tierra con respecto al resto del sistema solar)sea posible determinarlo dentro del conjunto, este conjunto en su totalidad puede estarse moviendo con respecto a cuerpos o conjuntos de cuerpos fuera del sistema considerado sin que ninguna condición.dentro del sistema o conjunto, pueda detectar tal movimiento, por ser común a todos los miembros del grupo.
Por ejemplo, podemos conocer todos los movimientos respectivos de los planetas dentro de nuestro sistema solar; pero nuestro sistema solar como un todo se mueve en relación al centro de nuestra galaxia, que a su vez se mueve con un conjunto de galaxias de las que forma parte y es posible continuar como en “un cuento de nunca acabar”.
Segunda: porque todas las ecuaciones de los cuerpos deben referirse a un único sistema de referencia. En nuestro caso
D32 = d3 – d2 del conjunto (1)
No está referida al sistema de referencia situado en c1, el sistema no puede ser resuelto y los desplazamientos intrínsecos no pueden ser hallados. Esto pudo ser deducido desde el comienzo, a priori, al tener en cuenta que el desplazamiento intrínseco del cuerpo donde situamos el sistema de referencia no puede ser detectado por éste.
Estamos lejos de comprender las consecuencias más profundas de la relatividad del movimiento,mas allá de la inmediata utilidad de sus más simples aplicaciones.
**********
LA NATURALEZA DEL ESPACIO.
EL ESPACIO ES EL QUE CONTIENE
TODOS LOS OBJETOS MATERIALES DEL MUNDO.
TODO LO QUE ES,
ES en EL ESPACIO.
¿Y POR ÉL?
La física cuántica nos da indicaciones de que sí,
y también, desde hace mucho, la mística.
EL ESPACIO ES EL QUE ESTABLECE
UN ORDEN POSICIONAL DE TODOS LOS OBJETOS.
EL ESPACIO ES LA EXTERIORIDAD
LO QUE HACE POSIBLE
LAS RELACIONES EXTRÍNSECAS ENTRE LOS OBJETOS.
AQUELLO DONDE LO QUE ES, PUEDE SER
y esta capacidad para permitir la expresión de existir conlleva la libertad de hacerlo en una multiplicidad de lugares, porque el espacio también organiza un orden en lo externo, de modo que lo que ES, se reconoce en su plena individualidad y en su capacidad de interactuar.
EL ESPACIO ES CONTINENTE Y LUGAR
PARA QUE PUEDA EXISTIR EL MOVIMIENTO.
Y TAMBIEN ES FUENTE Y SUMIDERO
DE TODO LO EXISTENTE
COMUNICACIÓN CON AQUELLO QUE SOSTIENE
TODO LO EXISTENTE
“EL ESPACIO ES UNA REPRESENTACIÓN
A PRIORI
QUE SIRVE DE FUNDAMENTO A TODAS LAS INTUICIONES EXTERNAS.”
Kant.
“Nunca se puede efectuar la representación sin que haya espacio,
si bien se puede pensar que en el espacio
no exista objeto alguno.”
Kant.
“El espacio, por tanto, debe ser considerado como:
LA CONDICION DE LA POSIBILIDAD DE LOS FENOMENOS
Y NO COMO UNA DETERMINACION DEPENDIENTE
DE ELLOS.”
Kant.
“y es una representación a priori, que es, necesariamente, el fundamento de los fenómenos externos.”
Kant.
una representación a priori es producto de la experiencia de toda la evolución en su interacción con el mundo hasta el organismo actual que estamos considerando.
Y si se quiere, subjetiva, porque es propia del sujeto; `pero todo lo objetiva que puede ser nuestra propia percepción de los objetos, pues tienen la misma génesis.
El espacio surge en forma instintiva como percepción, de nuestra herencia de evolución en el mundo; para enriquecerse en forma dramática a partir del uso de nuestra razón.
Los cuerpos y sus formas son apariencia, modos nuestros de percibir particulares estructuras de la materia en la escala espacio-temporal que nos es propia.
Espacio y cuerpos, todos comienzan siendo sensaciones; pero estas se hacen percepciones a través de la experiencia y la razón.
La experiencia ajusta nuestra subjetividad por relaciones de causa-efecto que en su uniformidad nos informan de un mundo regido por leyes.
El “no yo” no tiene un comportamiento físico para cada uno, dependiendo de su subjetividad. El “no yo” tiene el mismo comportamiento físico para todos, de allí su objetividad
El espacio puede considerarse como lugar o posición, recipiente, constituyente del mundo, y DIOS mismo, sin presentarse ninguna contradicción.
¿Es el espacio una propiedad de la materia, puesto que no es medible sin ella? Ya establecimos que NO.
TODO INFINITO A DE REFERENCIARSE
PARA PODER SER LOCALMENTE, MEDIDO.[14]
Esto es algo común a cualquier magnitud
y constituye una necesidad matemática.
¿Por qué la expresión relativa del espacio a de oponerse a su posibilidad de absoluto? ¿En que se estorban?
NI SE OPONEN NI SE ESTORBAN.
Su relatividad métrica es un signo de su infinitud.
Podemos concebir el espacio ausente de cuerpos. Es lo que llamamos el vacío dando a entender su capacidad para albergarlo con cuerpos;
PERO IDENTIFICABLE CON LA NADA
SOLO EN EL SENTIDO DE NUESTRA INCAPACIDAD PARA HABLAR DE ÉL.
LO QUE DE DIOS,ESTA MAS ALLA,
DE NUESTRA COMPRENSION.
Y QUE LA ELECTROCINAMICA CUÁNTICA
NOS PRESENTA EN LA ACTUALIDAD
COMO FUENTE Y SUMIDERO
DE LA SUSTANCIA EXISTENTE.
LA CONDICIÓN ABSOLUTA DE LA POSIBILIDAD
DE LOS OBJETOS EXTERNOS. DIOS MISMO
EL espacio se ha considerado desde la filosofía y la mística y aun por importantes matemáticos y científicos como una de las esencias del UNIVERSO, EL TODO, o DIOS.[15]La biblia dice de DIOS: “En el vivimos y nos movemos y somos” sentencia que solo se acomoda a el espacio, y al tiempo, otra de las esencias divinas considerada dentro de la mística,
“EL ESPACIO Y EL TIEMPO SON LA SUSTANCIA MISMA DEL UNIVERSO
Y DE DIOS
GUARDAN ENTRE SI LA MISMA RELACIÓN QUE EXISTE
ENTRE EL CUERPO Y EL ESPÍRITU.”
Manuel Alexander.
Desde este punto de vista, en efecto,
“EL ESPACIO SERIA EL CUERPO DE TODA LA REALIDAD,
POR LO TANTO DE DIOS MISMO
QUE ESTÁ EN LA SIMA DE TODA LA REALIDAD.”
Manuel Alexander (“Espacio, tiempo y deidad” 1920)
Esta cosmovisión satisface los impuestos de la razón, la belleza, la virtud y la mística. Y la consideramos satisfactoria.
Todo es ilusorio en cierto sentido, en fin de cuentas lo que tenemos del mundo son representaciones;
representaciones aproximadas,pero que encierran lo que el mundo ES.
Que desde la ciencia conocemos como un complejo de relaciones entre las magnitudes que medimos, y desde el sentimiento y la conciencia como estados que solo en el lenguaje del arte, de la fe, y del amor, podemos apenas expresar.
DESDE TODOS ELLOS SENTIMOS QUE
EL ESPACIO ES UNA DE LAS CLAVES DEL MUNDO.
BIBLIOGRAFIA:
(1) MECAMICA. Volumen 1.BERKELEY PHYSICS COURSE. Editorial Reverté S.A. 1968
(2) MECANICA. Francis W. Sears. E.R. 1968
(3) CURSO DE FISICA GENERAL. L. Landau, A. Ajiezer y E. Lifshitz. Editorial MIR 1984
(4) WIKIPEDIA 2013
(5) DINAMICA DE LAGRANGE. Dare A. Wells Mc Graw-Hill de México S.A. 1972
(6) LA BIBLIA.
(7) LECCIONES ACERCA DE LA VERDAD. H. EMILIE CADY. UNITE SCHOOL OF CRISTIANITY 1951
(8) DICCIONARIO FILOSOFICO. Nicolas Abbagnano. Fondo de la Cultura Económica. Segunda edición 1974.
(9) FUERZAS EN LA NATURALEZA. V. Grigóriev y G. Miákishev. Editorial MIR-Moscú 1986.
[1] Aquello de que están hechos los cuerpos.
[2] Conceptos a partir de los cuales se elabora toda una ciencia. Se les llama primarios porque no son demostrables, ni plenamente definibles generalmente son muy intuitivos y parecen obvios. Los resultados de su aplicación hablarán a favor o en contra de los mismos y modificarán su acepción.
[3] Llamaremos micromundo el existente en el volumen de espacio interior al átomo, especialmente el de su núcleo.
[4] Isótropo: que presenta las mismas propiedades, en cualquier dirección que sigamos, a partir de cualquier punto.
[5] La unidad astronómica es aproximadamente igual a 149.6 millones de kms.
[6] Cualquier plano contenido en el mismo es euclidiano, o de curvatura infinita.
[7] La desviación de la luz al pasar cerca de grandes masas o el perihelio en la órbita del planeta Mercurio debido a su cercanía al sol.
[8] En la teoría general de la relatividad.
[9] Un año luz es igual a 9.46 X 1000000000000Km.
[10] MECANICA. Berkeley physics course. Patrocinado por el National Science Foundation. Volumen 1. Editorial Reverte 1968.
[11] En capítulos posteriores discutiremos estas magnitudes en detalle.
[12] Las situadas sobre los polos norte o sur.
[13] que se mueven uniformemente. (sin aceleración)
[14] Considérese por ejemplo una simple recta.
[15] Para algunos, entre los que nos incluimos, es lo mismo. Otros que establecen diferencias debían analizar los innumerables puntos de contactos de sus conceptualizaciones; pero sabemos que esto será difícil para teos y ateos.
